Line Emission [EotW]
Spectral lines are a ubiquitous feature of astronomical data. This week, we explore the special case of optically thin emission from low-density and high-temperature plasma, and consider the component factors that determine the line intensity.
The flux [ergs s-1 cm-2 sr-1] from an optically thin emission line that arises due to a transition between energy levels j and i in an ionic species Z+I is simply written. It is the product of the probability of the transition Aji(Z,I) (aka the Einstein coefficient), the number of particles of the species that exists in the upper level of the transition Nj(Z,I), the volume of the emission dV, and the energy of the emitted photon hc/lambda, scaled down by the distance to the source (4 pi d2; note that the factor 4 pi is due to the emission being radially symmetric).
But this apparently purely atomic calculation can be reformed and rewritten, after some algebra, in terms of quantities that are astrophysically more meaningful. The equations below walk you through the tranformation from atomic physics to quantities that can be separated out into different hierarchies of astrophysical source properties, from things that change not at all from one source to another, to things that are likely not the same even along the line-of-sight.
All of the quantities that depend only on the atomic physics can be pulled together into the emissivity of the transition, eji(Ne,Te,Z,I). This is (mostly) independent of the physical conditions at the source, and is generally treated as invariant except for changes due to the electron number density. These can therefore be calculated beforehand, and indeed, codes such as CHIANTI, SPEX, and APEC do just that. The abundance AZ (note, not the Einstein coefficient: apologies for the overlapping notation, can’t be helped for historical reasons) changes from source to source, and sometimes even within a source, but is the stablest of the factors after the emissivity. The ion balance i(Te,Z,I)=NZ,I/NZ is strongly variable, as is the so-called emission measure, EM = Ne2dV, which btw is also a function of Te. The atomic emissivity and the ion balance are sometimes combined together and the product is also confusingly referred to as the emissivity. Strictly speaking, the level population is dependent on the ion fractions and therefore the emissivity cannot be exactly separated from the ion balance. However, this dependence is weak in the density limits we are usually interested in (Ne~108-12 cm-3, as in the solar corona), and the two can be separated.
It is important to note that each of the terms listed above have associated model or measurement uncertainties. Often, the Einstein coefficients and the energy of the emission are not experimentally verified, and the level populations are approximate calculations due to the complexity of the level structure of the species in question. Typical ion balance calculations assume that the plasma is in thermodynamic equilibrium, which is often not a good assumption. Abundances are known to vary radically (by factors greater than 2x) across the source. And finally, except at high temperatures and low density (such as stellar coronae), the assumption of zero opacity (i.e., that any emitted photon escapes to infinity without any scatterings) is not applicable, and radiative transfer effects must be included.
A brief word about the units. Astronomers tend to use cgs, not SI. So the flux usually has units [ergs/s/cm2/sr], the emissivity eji is in [ph cm3/s] (unless the factor hc/lambda is included in the emissivity, in which case the units are [ergs cm3/s]), and the emission measure is in [cm3].
The emission measure is a story by itself, one best left alone for another time.
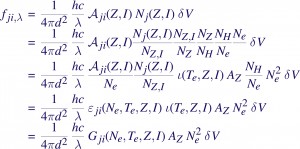
hlee:
Irrelevant, but I want to share my experience from an astronomy class (SP ’08) taught by Prof. Finkbeiner at Harvard. As the semester approached to the end, the professor asked students topics to be covered, one of them was MCMC. I became curious how he’ll introduce and cover the vast world of MCMC to students in an hour or so. I thought he’ll start with Bayes theorem, which easily bore off students at the beginning (Although Bayes theorem is prevailed in daily life either consciously or unconsciously, when it comes to a theorem nobody gets excited). I think he was brilliant. He began his lecture from detailed balance (derived from these line emission equations if I recall correctly) to reach posterior ~ likelihood*prior without saying much about the statistical definitions of likelihoods, priors, and posteriors. Since the integrations basically require MCMC methodologies, he made a smooth transition and introduced Gibbs sampling and Metropolis-Hasting algorithm.
The reason for telling my experience is that there is quite statistics about your post, although the equations are purely based on (atomic) physics.
05-14-2008, 5:34 pmTomLoredo:
Hyunsook, that’s an encouraging story—that MCMC is being taught so effectively to astronomers at Harvard. As you noted, there’s nothing about MCMC that is particularly Bayesian (in fact, even Bayesian use of it is typically frequentist in flavor), so there’s no need to start with Bayes’s theorem. After all, (Bayesian) statisticians “borrowed” MCMC from statistical physics, where it had been flourishing in non-statistical problems since the time of Metropolis et al..
Fundamentally, MCMC is just a way to build a pseudo-random number generator; the algorithm is a Big Deal because it lets you build one for complicated, multivariate distributions in an apparently straightforward fashion. (I say “apparently straightforward” because there’s lots to worry about in the actual implementation for complex problems, even though the Metropolis-Hastings algorithm most commonly used for MCMC is incredibly simple.) It just so happens that Bayesian calculations often require integrals of complicated, multivariate distributions, so MCMC has become closely associated with Bayes.
One of my first introductions to MCMC was a review paper by D. Toussaint, “Introduction to algorithms for Monte Carlo simulations and their application to QCD” (Computer Physics Communications, v56, 69-92 (1989)). The first few pages have a physics-flavored intro to the basic ideas of MCMC, motivated by problems in statistical physics and lattice QCD (not a prior or likelihood in sight!). I still send astronomer and physicist colleagues to this paper (among others), to see MCMC ideas in our language. As with Finkebeiner’s lecture, a key element in Toussaint’s presentation is detailed balance. It’s a nice paper, taking the reader from basic Monte Carlo to the Metropolis algorithm, Langevin methods, and ultimately hybrid Monte Carlo, in not very many pages.
(It’s perhaps worth noting that reversibility (detailed balance) is a sufficient but not necessary condition for a Markov chain to have a desired target distribution be its stationary distribution. There has been very little exploration of non-reversible algorithms; Diaconis, Holmes and Neal had a paper on this not long ago.)
05-22-2008, 12:00 am