Links (all on Optics Twiki so acct/passwd needed)

• HRMA effective area meeting main page
• Pileup primer and references
• Diab's overview of MC and probabilistic methods, and summary of results (pdf)
• Code, manual, and other files for probabilistic method

Summary

Our original analysis (c. 1998) of the XRCF Carbon-continuum SSD measurements only included the Phase E measurements (1000 s on each shell), and used approximate corrections for pileup, since accurate modeling was beyond our mental and computer-power capabilities of the time. The new analyses use two approaches: probabilistic and Monte Carlo (by Diab). The former method has been applied to the 4 phase-E measurements, plus 1 phase-C all-shell measurement (aperture position was about 1 mm off, so not useful), 4 phase-D measurements (results similar to phase E but with only about 1/4 the counts), and phase-D measurements for shells 1 and 3 using 500-um apertures instead of the standard 2-mm apertures. (There was a data collection failure for ssd_x with Shell 4.) There are additional sets of phase-D measurements using even smaller apertures, but these were not deemed to be worth the effort.

The probabilistic method is much faster than the Monte Carlo method for modeling 2-event pileup and deadtime (~10 seconds to run) but takes over an hour for 3-event pileup. I therefore iterated the 2-event modeling several times to get a nearly final result and then ran once or twice with 3-event modeling to obtain the final answer. The MC method takes less than 1 hour (?) to run and treats all orders of pileup at once. It does not, however, include iteration/convergence capabilities so we used the probablistic method to `de-pile' the SSD spectra and then confirmed those results with the MC method.

The final results are not very different from what we got in 1998--a percent or two here and there, somewhat more at very high energies where pileup is more significant. Ping Zhao will present a comparison of HRMA EA's derived from the new and old analysis results.

Model Parameters

Diab has already outlined the modeling methodology (see pdf above). The (slow) shaping amplifier output pulse profile for a 2-us shaping time was previously obtained from an oscilloscope trace with 0.1-us time intervals. Note that the trace must be carefully smoothed to avoid problems with spurious peak-finding.

Parameter	Description	How determined	Value
Twide	Slow amp pulse width = PUR inspection time interval	Number of modeled output pulser counts must match obs'd	19.5±0.5 us for ssd_x
Tfast	Fast discriminator output pulse width	Make model pulser/X-ray pileup match obs (espec. true pileup)	1.0±0.1 us
Tpeak	Time for shaping amp output pulse to reach maximum	Read from oscilloscope trace	4.0±0.1 us
PURlim	PUR (fast discriminator) threshold	Make model pulser/X-ray pileup match obs (espec. tail pileup)	Channel 256±4 (1280±20 eV) for ssd_x
MCB LLD	ADC lower level discrimanator	Lowest channel in acq*.pha file	Variable, usually around channel 58
MCB Tdead	ADC processing deadtime (after pulse max is found)	Ortec manual	1.5 us

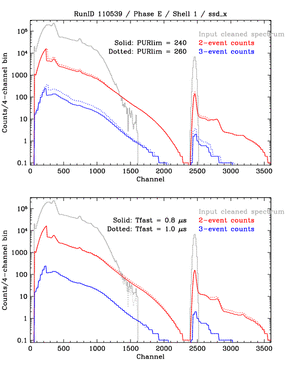
Left: Illustration of sensitivity of model output to the PUR rejection threshold (PURlim) and fast discriminator pulse width (Tfast). Values of PURlim and Tfast were determined by comparing model output to the observed spectrum in selected channel ranges, mostly lying above the pulser peak where all events come from pileup (at least for shells 1, 3, and 4). Twide was determined by requiring that the number of output pulses match the observed number; the number of input pulses has a known value.
Right: Comparison of results (total simulated counts using identical input spectra) using Probabilistic and Monte Carlo methods. Traces end where the number of counts per 4-channel bin falls below 100. Agreement is excellent throughout the relevant energy range for each shell, although disagreements grow toward higher energies where pileup dominates the total number of counts; there are also some minor disagreements below the PUR threshold.

Parameters for ssd_x were determined from modeling the phase E data, which had by far the best statistics. The parameters also did a good job for the phase C and D ssd_x data (see plots). It was difficult to determine the best parameters for ssd_5 data. In some cases it appears that the shaping time was not the recorded value, but the ssd_5 rates were so low that pileup was negligible and all that matters is that the deadtime make the model match observation. In fact, the standard pulser_out/pulser_in deadtime correction method is completely adequate.

Model and Observed Spectra

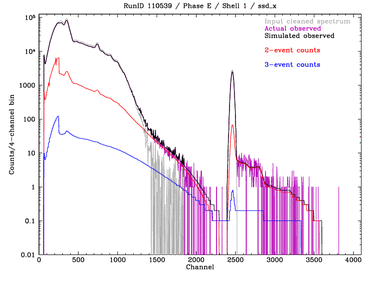
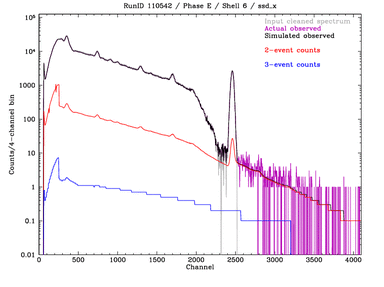
Phase E Carbon-continuum measurements with SSDs; Shells 1,3,4,6 with ssd_x. The gray curve is the final "result," i.e., what the spectrum would look like without any pileup or deadtime. This is used as the model input. 1 channel = 5 eV.

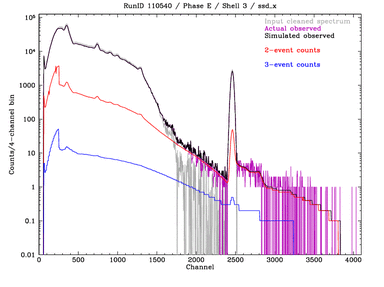
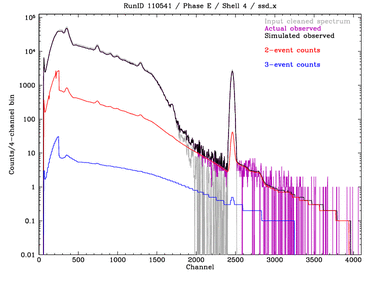
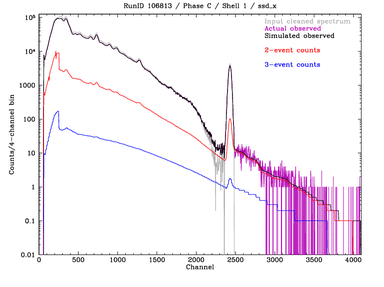
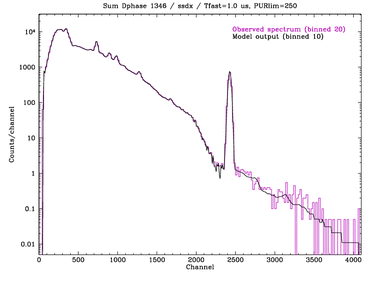
Same plots (+ssd5 from below) but including the rejected 2- and 3-event counts:

• Shell 1
• Shell 3
• Shell 4
• Shell 6
• SSD_5

Left: Phase C all-shell measurement, ssd_x.
Right: Phase D, ssd_x summing results from all 4 shells. These plots show that using the pileup parameters determined from analysis of Phase E data works well for the Phase C and D data, too.

Summed ssd_5 spectrum from 4 Phase E measurements. Rates in ssd_5 were much lower than in ssd_x and so there was virtually no pileup. Deadtime was also very small so the black, purple, and gray curves lie essentially on top of each other.

Comparison with Previous Analysis Results

In the figure below, the top panel shows model output divided by input. If there were no pileup this would be a flat line equal to the the detector livetime. The bottom panel shows the same curves normalized to the pulser peak livetime, revealing the net pileup correction factors. The old (1998) correction factor for shell 1 is also shown; the other old correction curves are not shown to avoid clutter.

The old corrections were obtained using the pulser/X-ray pileup counts to make a rate-dependent event redistribution function. As you can see, it wasn't bad. (Also keep in mind that computers are ~100 times faster now so the more accurate analysis done here would not have been feasible in 1998, especially since many runs were necessary to test and debug the code.) The large differences between old and new below around channel 300 (1500 eV) are because the old analysis could not account for the PUR threshold, but this doesn't matter because results below that energy aren't useful anyway because of uncertainties in detector icing (i.e., QE).

Top: Model output divided by input spectrum, showing the effective energy-dependent livetime.
Bottom: Same curves normalized to the pulser peak livetime, revealing net pileup correction factors, including the corresponding curve for the 1998 shell 1 analysis.